Longitudinal Data Analysis of Continuous and Discrete Responses for Pre post Designs

Analysis of Longitudinal Data Continuous Response: Part 1 Usha Sambamoorthi 1, 2, 3 1 HSR& D Center, East Orange VA 2 School of Public Health, UMDNJ 3 IHHCPAR, Rutgers University 08 April 2005 1

Objectives u Mention various methods of analyzing longitudinal data u Non-statistical view point u Build and develop mixed effects models using PROC MIXED procedure in SAS u interpret findings 2

At the end of this session you will learn u Know u about fixed effects, random effects graphical data analysis using SAS Proc GPLOT u To build models using SAS Proc mixed u To read SAS Proc mixed output u how u to to interpret findings summarize results for publications 3

Types of Longitudinal Data Repeated Cross-sections u Different samples are taken at each measurement time, to measure trends not individuals experiences Examples u National Health Interview survey (NHIS) u Behavioral Risk Factor Surveillance Study (BRFSS) 4

Types of Longitudinal Data Time Series u Collection of data Xt (t = 1, 2, …, T) with the interval between Xt and Xt+1 being fixed and constant. In time-series studies, a single population is assessed with reference to its change over the time u Here we measure trend, seasonality EXAMPLES u Daily, weekly, or monthly performance of a stock u Daily pollution levels in a city u Annual measurements of sun spots 5

Types of Longitudinal Data Panel or Multi-level Data u Same individual/subject/unit is observed over two or more time points. Typically large number of observations repeated over a few time points i = 1, 2, 3…. N t = 1, 2, 3… T Examples u Medical Expenditure Panel Survey – Households followed over a period of 2 years – 5 rounds u Medicare Current Beneficiary Survey – Individuals followed for a maximum of 4 years 6

Types of Longitudinal Data Clustered or Hierarchical Data u The observations have a multi-level structure (Same patients (i) from facilities (k) followed over time (t)) k = 1, 2, 3…. K i = 1, 2, 3…. N t = 1, 2, 3… T Example u Minimum Data Set (MDS) – Quarterly and Annual clinical information on nursing home residents 7

Types of Responses in Longitudinal Data u Continuous – Cost of health care u Discrete – Use or non-use of mental health services u count – number of outpatient visits u survival – time from diagnosis to death 8

Challenges in Analyzing Longitudinal Data Account for dependency of observations u Both dependent and independent variables change over time –time varying covariates u Invariable presence of missing data u u Analysis on completers u Last observation carried forward (LOCF) 9

Designs of Longitudinal Data u Equally spaced or balanced panel data u When each subject is scheduled to be measured at the same set of times (say, t 1, t 2, …, tn), then resulting data is referred as equally-spaced or balanced data u Unequally spaced or unbalanced data u When subjects are each observed at different sets of times u there are missing data 10

Traditional models (OLS) can not be applied to Longitudinal data OLS Model Assumes residuals are independently distributed (ie no correlation); E ( i, j) = 0 u Consequences when this assumption is violated u OLS co-efficient estimates are not biased u OLS estimates do not have the minimum variance; inefficient estimates (Standard errors may be large) u biased tests of hypothesis leading to incorrect conclusions u In longitudinal data repeat observations within a subject are usually correlated over time u Variances within subjects can vary over time 11

Traditional models (OLS) can not be applied to Longitudinal data assumes homoskedasticity; E ( i 2 ) = 2 u Consequences when this assumption is violated u OLS co-efficient estimates are not biased u OLS estimates do not have the minimum variance; inefficient estimates (Standard errors may be large) u biased tests of hypothesis leading to incorrect conclusions u In longitudinal data variances within subjects can vary over times 12

Effect of violating OLS assumptions on standard error estimates of independent variables u If there is positive correlation of observations within a subject u Time-independent explanatory variables: gender, race/ethnicity u Standard error estimates will be underestimated u Leads to incorrect tests of significance u Time-varying covariates: blood pressure values, severity of illness, drug use u Standard error estimates will be overestimated u Leads to incorrect tests of significance 13

Requirements for Longitudinal Models u capture trend over time while taking account of the correlation that exists between successive measurements u describe the variation in the baseline measurement and in the rate of change over time u Explain the variations in baseline measurement and trends by relevant covariates 14

Analysis Considerations for Longitudinal Data u Balanced or equally spaced vs unbalanced data u Type of dependent variable – Continuous, non-normal (counts), ordinal (poor to excellent health), nominal (binary) u # of subjects – more advanced models are based on large sample theory – N < 30 ? ? ? u # and type of covariates u Selecting possible covariance structure u # of observations per subject u If only 2, compute change scores, use simple methods 15

Minimum time periods 1) A minimum of 4 time points is recommended; With < 4 time points, it is not possible to identify enough parameters in the growth model to make the model flexible 2) 4 time points give more power 3) with 3 time points restrictions need to be placed on the growth models 16

Models for longitudinal data 1. Derived variable approach – summary score, change score. . 2. ANOVA for repeated measures (assumes compound symmetry – constant variance and covariance over time) • Allows for different intercepts – but no time trend (subjects can deviate only in baseline measures but consistent thereafter) 3. MANOVA for repeated measures ( does not permit missing data, or different measurement periods for subjects) 4. Mixed Effects Models – Applicable to all types of outcomes (normal, non-normal, categorical) – Robust to missing data (irregularly spaced observations) – Can handle both time-variant and time-invariant covariables 17

Models for longitudinal data 5. Covariance Pattern Models – Does not distinguish "within" and "between" subject variation 6. Generalized Estimating Equation (GEE) Models – missing data are only ignorable if the missing data are explained by covariates in the model 18

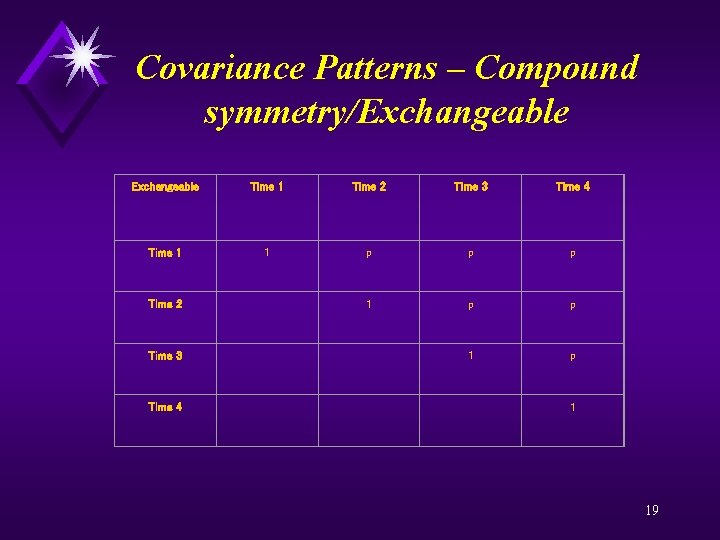
Covariance Patterns – Compound symmetry/Exchangeable Time 1 Time 2 Time 3 Time 4 Time 1 1 p p p Time 2 1 p p Time 3 1 p Time 4 1 19

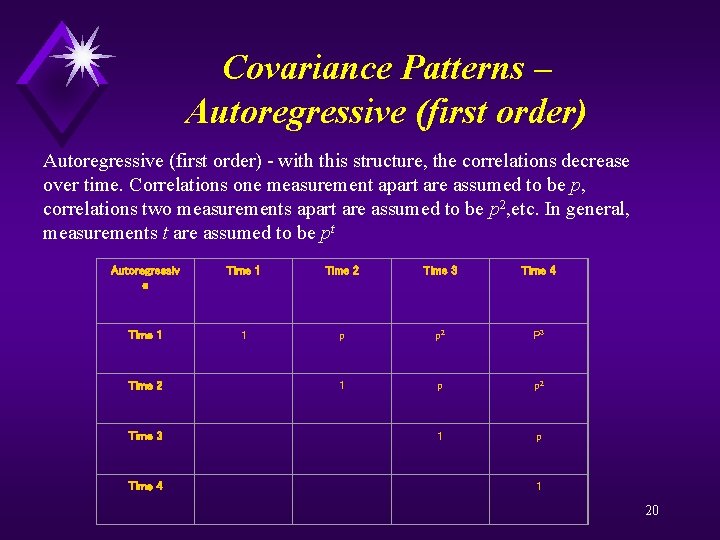
Covariance Patterns – Autoregressive (first order) - with this structure, the correlations decrease over time. Correlations one measurement apart are assumed to be p, correlations two measurements apart are assumed to be p 2, etc. In general, measurements t are assumed to be pt Autoregressiv e Time 1 Time 2 Time 3 Time 4 Time 1 1 p p 2 P 3 Time 2 1 p p 2 Time 3 1 p Time 4 1 20

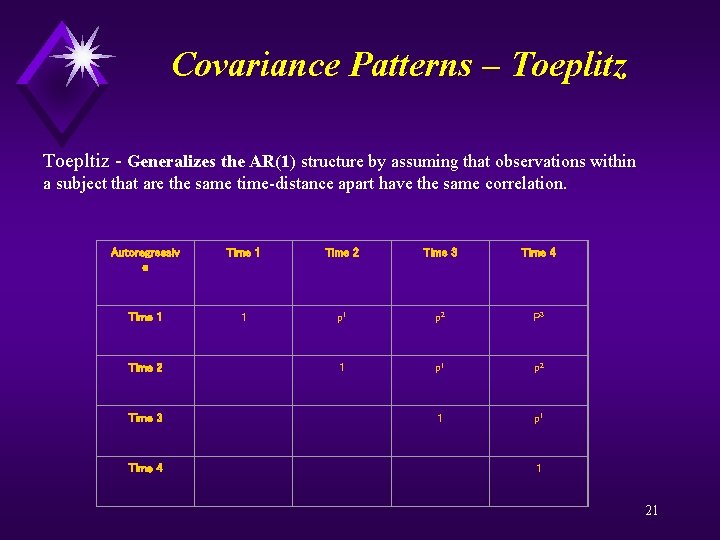
Covariance Patterns – Toeplitz Toepltiz - Generalizes the AR(1) structure by assuming that observations within a subject that are the same time-distance apart have the same correlation. Autoregressiv e Time 1 Time 2 Time 3 Time 4 Time 1 1 p 2 P 3 Time 2 1 p 2 Time 3 1 p 1 Time 4 1 21

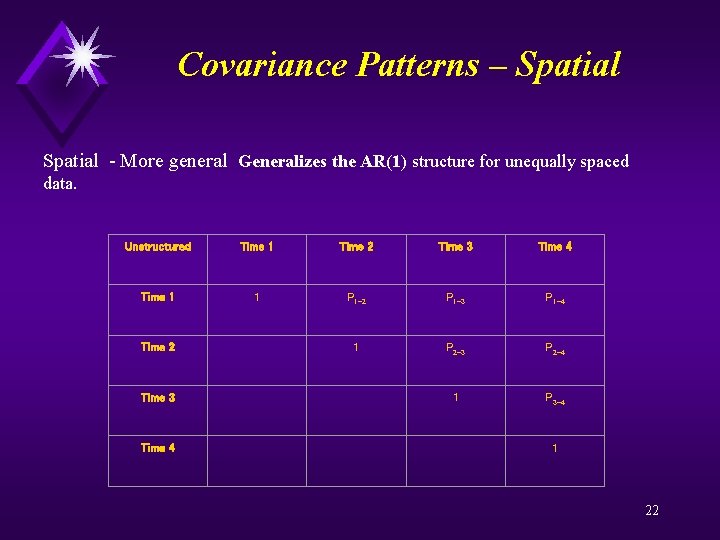
Covariance Patterns – Spatial - More general Generalizes the AR(1) structure for unequally spaced data. Unstructured Time 1 Time 2 Time 3 Time 4 Time 1 1 P 1 -2 P 1 -3 P 1 -4 Time 2 1 P 2 -3 P 2 -4 Time 3 1 P 3 -4 Time 4 1 22

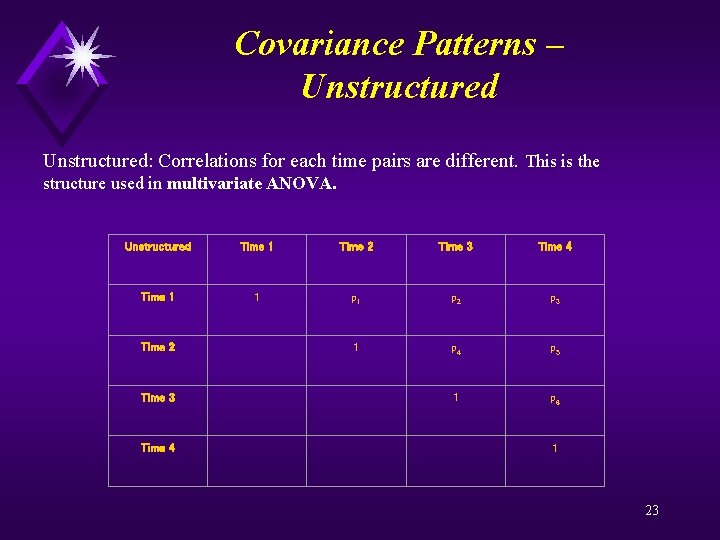
Covariance Patterns – Unstructured: Correlations for each time pairs are different. This is the structure used in multivariate ANOVA. Unstructured Time 1 Time 2 Time 3 Time 4 Time 1 1 p 2 p 3 Time 2 1 p 4 p 5 Time 3 1 p 6 Time 4 1 23

Selecting Covariance Patterns Choose relevant structure Not all structures are applicable to all data Equal spacing: CS, Unstructured AR(1) Toeplitz Spatial Unequal Spacing: CS UN Spatial 24

Fixed Effects – Least Square Dummy Variable Model u u LSDV approach takes care of within subject correlation by using dummy variables for class effects u To capture individual effect, individual dummies are included; If there are 100 individuals, 99 dummy variables representing 99 individuals are included; To capture time effect, time dummies are included; if there are 10 time periods, 9 time dummies are included Cons u Large number of observations needed, DF quickly reduced u Time-constant covariates such as gender can not be included 25

Mixed Effects Models means and variances / covariances Has both random and fixed effects What is a fixed effect? Each person is unique ; has his/her own baseline and growth trajectory In terms of covariates – they represent all the values in the population If A, B, C are drugs, they are do not represent a random sample of drugs from a population; so the inferences are applicable for only A, B, C and not drug D 26

Random Effects For each unit, baseline value is the result of a random deviation from some mean intercept. The intercept is drawn from some distribution for each unit, and it is independent of the error for a particular observation; we just need to estimate parameters describing the distribution from which each unit's intercept is drawn Facilities – could be considered as random if they are random sample from a population 27

When to use Fixed vs Random Effects u Depends on research question u When to use fixed effect? If interested in the mean of an outcome contains all values Example: Race, Gender, Age u When to use random effect? If interested in the variance of an outcome Sampled from a population of values Example: Facilities, nursing homes, time 28

Data Source u 104 Respondents u Respondents are interviewed in 4 waves u Interval between interviews varied across observations u Both time varying and time-invariant characteristics 29

Study Objectives Within person comparisons 1. How does an individual's vitality change over time? 2. What is the rate of change? Between person comparisons 3. How is the change in vitality level associated with comorbid FM and age? 4. Do individuals with out comorbid FM have more stable baseline and change rate than those with comorbid FM? 5. How do we summarize these results for a journal article? 30

Measures: Dependent and Independent Variables Time Invariant Ø Presence of Comorbid FM Ø Ø Ø Yes No Age (continuous) Ø Ø Baseline Age Varies from xx to xxx Time Variables Ø Ø Becker Depression Inventory Score Ø Ø Range 0 to xxx Xx items Dependent Variable # of interviews (waves) Ø Ø Ø Time Varying covariates 1 -4 1 person had 3 interviews SF-36 Vitality Score Time Ø Ø Baseline coded as zero Time since baseline measured in months 31

Building models 1. Exploratory data analysis – Descriptive statistics, individual group profiles, plots 2. Begin with simple models and build towards more complex models 3. Decide fixed and random components 4. Select covariance structure 5. Model diagnostics 32

Organize/list data proc print data=a(obs=25); title 'Line Listing of Vitality Data' ; run; Line Listing of Vitality Data Obs id flup fm time age sf_vt bdi_deprn 1 10029 1 0 0. 00 45. 49 70 2 2 10029 2 0 9. 38 45. 49 55 0 3 10029 3 0 16. 33 45. 49 45 2 4 10029 4 0 25. 90 45. 49 70 0 5 10057 1 0 0. 00 57. 95 10 5 6 10057 2 0 9. 11 57. 95 5 0 7 10057 3 0 22. 36 57. 95 25 13 8 10057 4 0 30. 13 57. 95 5 13 9 10138 1 0 0. 00 47. 60 5 2 10138 2 0 6. 85 47. 60 15 0 11 10138 3 0 15. 70 47. 60 25 2 10138 4 0 24. 26 47. 60 30 1 13 10155 1 0 0. 00 33. 39 15 0 14 10155 2 0 5. 70 33. 39 0 9 15 10155 3 0 12. 33 33. 39 10 13 16 10155 4 0 18. 98 33. 39 10 0 17 10163 1 1 0. 00 47. 35 5 17 18 10163 2 1 11. 21 47. 35 0 0 19 10163 3 1 28. 43 47. 35 5 17 20 10163 4 1 36. 79 47. 35 0 14 21 10185 1 0 0. 00 43. 32 10 11 22 10185 2 0 8. 98 43. 32 25 23 10185 3 0 20. 16 43. 32 15 22 24 10185 4 0 35. 93 43. 32 25 0 25 10221 1 1 0. 00 36. 92 5 4 33

Check data proc means data=a maxdec= 2 n min max mean median std; title 'Descriptive Statistics vitality data' ; run; Descriptive Statistics vitality data The MEANS Procedure Variable Label N Minimum Maximum ƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒ id Case ID 239 10029. 00 10880. 00 flup Followup nbr 239 1. 00 4. 00 fm FM 239 0. 00 1. 00 time 239 0. 00 38. 66 age at baseline 239 26. 65 57. 95 sf_vt SF-Vitality 239 0. 00 70. 00 bdi_deprn Becker Depression inventory 239 0. 00 38. 00 ƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒ Variable Label Mean Median ƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒ id Case ID 10597. 84 10656. 00 flup Followup nbr 2. 51 3. 00 fm FM 0. 51 1. 00 time 12. 86 12. 30 age at baseline 43. 01 44. 30 sf_vt SF-Vitality 16. 88 15. 00 bdi_deprn Becker Depression inventory 10. 49 9. 00 ƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒ Variable Label Std Dev ƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒ id Case ID 209. 78 flup Followup nbr 1. 12 fm FM 0. 50 time 10. 06 age at baseline 7. 93 sf_vt SF-Vitality 15. 82 bdi_deprn Becker Depression inventory 8. 59 ƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒ Inference: • 1 to 4 waves • 51% had FM • Vitality ranged from 0 70 Maximum; large variation • time of follow up 38 months • Age range: 26 to 58 years 34

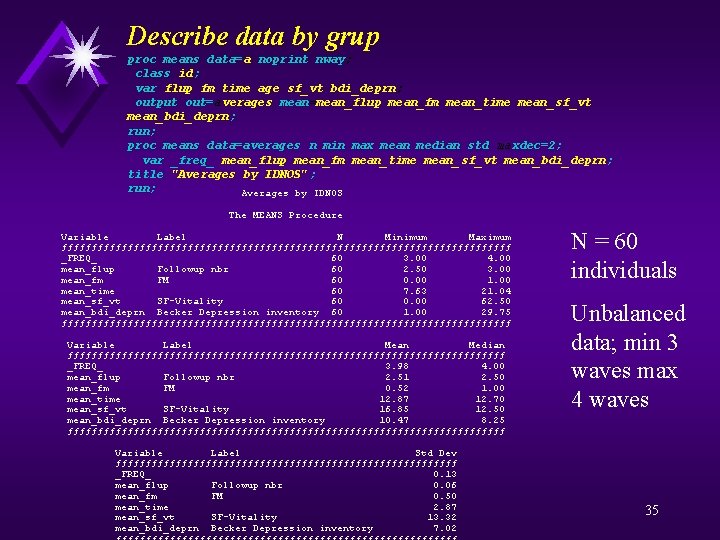
Describe data by grup proc means data= a noprint nway; class id; var flup fm time age sf_vt bdi_deprn; output out=averages mean=mean_flup mean_fm mean_time mean_ sf_vt mean_bdi _deprn; mean_bdi_ deprn; run; proc means data=averages n min max mean median std maxdec =2; maxdec=2; var _freq_ mean_flup mean_fm mean_time mean_ sf_ _ vt mean_bdi _deprn; mean_ sf mean_bdi_ deprn; title "Averages by IDNOS" ; run; Averages by IDNOS The MEANS Procedure Variable Label N Minimum Maximum ƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒ _FREQ_ 60 3. 00 4. 00 mean_flup Followup nbr 60 2. 50 3. 00 mean_fm FM 60 0. 00 1. 00 mean_time 60 7. 63 21. 04 mean_sf_vt SF-Vitality 60 0. 00 62. 50 mean_bdi_deprn Becker Depression inventory 60 1. 00 29. 75 ƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒ Variable Label Mean Median ƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒ _FREQ_ 3. 98 4. 00 mean_flup Followup nbr 2. 51 2. 50 mean_fm FM 0. 52 1. 00 mean_time 12. 87 12. 70 mean_sf_vt SF-Vitality 16. 85 12. 50 mean_bdi_deprn Becker Depression inventory 10. 47 8. 25 ƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒ Variable Label Std Dev ƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒ _FREQ_ 0. 13 mean_flup Followup nbr 0. 06 mean_fm FM 0. 50 mean_time 2. 87 mean_sf_vt SF-Vitality 13. 32 mean_bdi_deprn Becker Depression inventory 7. 02 N = 60 individuals Unbalanced data; min 3 waves max 4 waves 35

Averages by Time – SAS code proc sort; by flup; proc means data=a maxdec=2 noprint; by flup; var fm time age sf_vt bdi_deprn; output out=average; data average; set average; if (_stat_ = "N") then order = 1; if (_stat_ = "MEAN") then order = 2; if (_stat_ = "STD") then order = 3; if (_stat_ = "MIN") then order = 4; if (_stat_ = "MAX") then order = 5; proc sort; by order; proc print data=average; var flup _stat_ time sf_vt bdi_deprn; format time sf_vt bdi_deprn 5. 2; Title "Averages by Interview Waves"; run; quit; 36

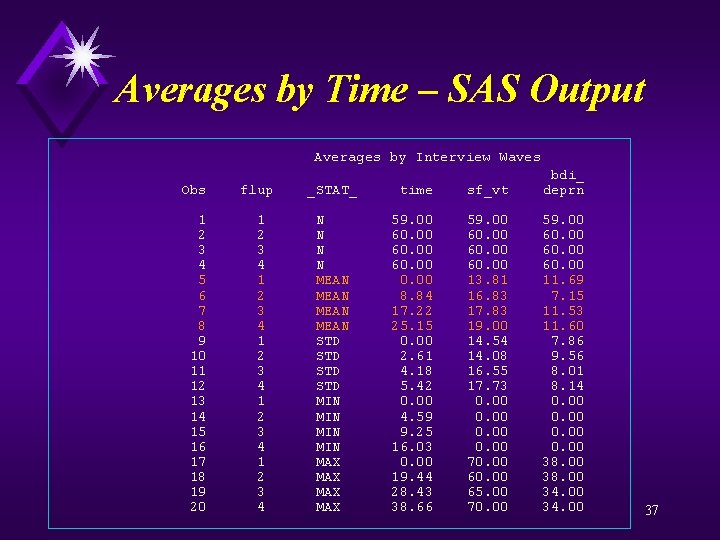
Averages by Time – SAS Output Averages by Interview Waves bdi_ Obs flup _STAT_ time sf_vt deprn 1 1 N 59. 00 2 2 N 60. 00 3 3 N 60. 00 4 4 N 60. 00 5 1 MEAN 0. 00 13. 81 11. 69 6 2 MEAN 8. 84 16. 83 7. 15 7 3 MEAN 17. 22 17. 83 11. 53 8 4 MEAN 25. 15 19. 00 11. 60 9 1 STD 0. 00 14. 54 7. 86 10 2 STD 2. 61 14. 08 9. 56 11 3 STD 4. 18 16. 55 8. 01 12 4 STD 5. 42 17. 73 8. 14 13 1 MIN 0. 00 14 2 MIN 4. 59 0. 00 15 3 MIN 9. 25 0. 00 16 4 MIN 16. 03 0. 00 17 1 MAX 0. 00 70. 00 38. 00 18 2 MAX 19. 44 60. 00 38. 00 19 3 MAX 28. 43 65. 00 34. 00 20 4 MAX 38. 66 70. 00 34. 00 37

Individual Profiles – SAS code goptions reset=all; proc gplot data=a; plot sf_vt*time=id / haxis = 0 to 40 by 5 vaxis = 0 to 70 by 10 nolegend; symbol v=none repeat=60 i=join color=red; label time="time from baseline"; title "Individual profiles vitality over time"; run; quit; 38

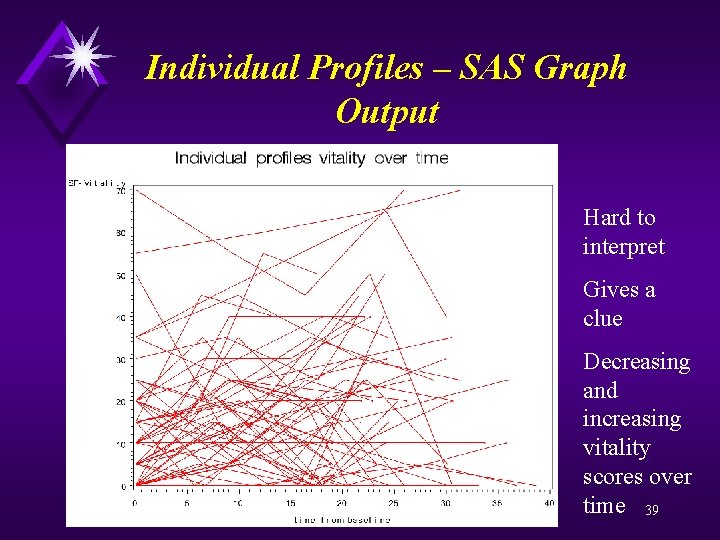
Individual Profiles – SAS Graph Output Hard to interpret Gives a clue Decreasing and increasing vitality scores over time 39

Average Trend Spline Smoothing – SAS code goptions reset=all; proc gplot data=a; plot sf_vt*time=ID / haxis = 0 to 40 by 5 vaxis = 0 to 70 by 10 nolegend; plot 2 sf_vt*time / haxis = 0 to 40 by 5 vaxis = 0 to 70 by 10 nolegend; symbol 1 v=none repeat=60 i=join color=red; symbol 2 v=none i=sm 50 s color=green width=5; label time="Months since baseline"; title "Average trend spline smoothing"; run; 40 quit;

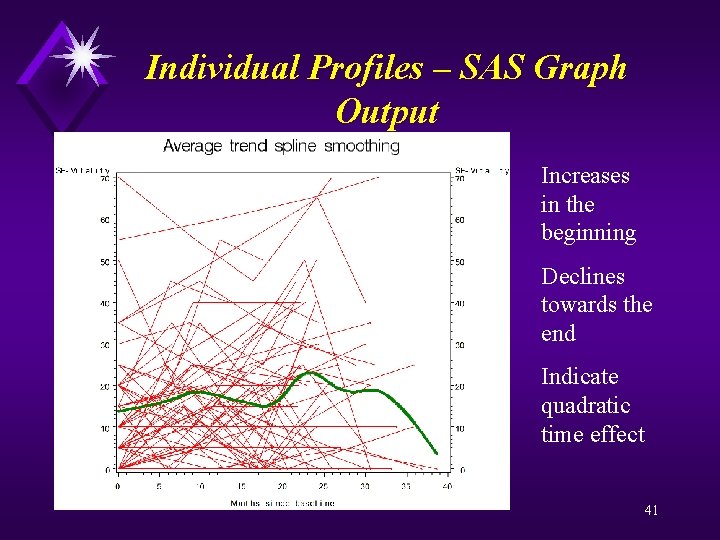
Individual Profiles – SAS Graph Output Increases in the beginning Declines towards the end Indicate quadratic time effect 41

Profiles and Average Trend (Linear, quadratic, cubic fits, spline smoothing – SAS Code) goptions reset=all; proc gplot data=a; plot sf_vt*time=1 sf_vt*time=2 sf_vt*time=3 sf_vt*time=4 / haxis = 0 to 40 by 5 vaxis = 0 to 70 by 10 nolegend overlay; plot 2 sf_vt*time=ID / haxis = 0 to 40 by 5 vaxis = 0 to 70 by 10 nolegend; symbol 1 v=none i=rq color=cyan width=3; symbol 2 v=none i=sm 50 s color=green width=3; symbol 3 v=none i=rc color=magenta width=3; symbol 4 v=none i=r color=black width=3; symbol 5 v=none repeat=60 i = join color=red; label time="Months since baseline"; title "Spline/linear/Quadratic/Cubic Trend"; run; quit; 42

Profiles and Average Trend (Linear, quadratic, cubic fits, spline smoothing – SAS graph output) Inference: Smoothing and different fits help see the pattern of average trend 43

Profiles and Comorbid FM – SAS Code proc format; value fm 1 = "Yes" 0 = "NO fm"; goptions reset=all; proc gplot data=a; plot sf_Vt*time=id / haxis = 0 to 40 by 5 vaxis = 0 to 70 by 10 nolegend; plot 2 sf_vt*time=fm / haxis = 0 to 40 by 5 vaxis = 0 to 70 by 10; symbol 1 v=none repeat=60 i=join color=red; symbol 2 v=none i=sm 50 s color=green width=3 line=1; symbol 3 v=none i=sm 50 s color=blue width=3 line=2; format fm fm. ; label time= "Time since baseline"; title "Individual Profiles with Presence/Absence of Comorbid FM"; run; quit; 44

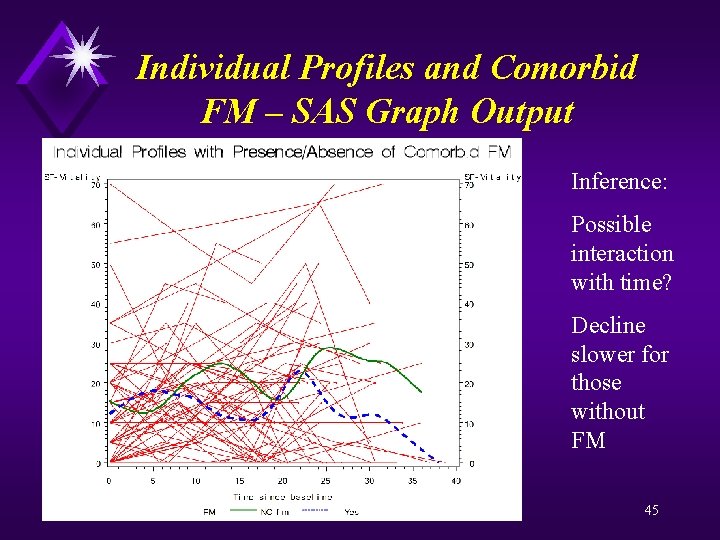
Individual Profiles and Comorbid FM – SAS Graph Output Inference: Possible interaction with time? Decline slower for those without FM 45

Profiles by Age - SAS Code proc format; value agegrp 0 - 35 = "0 -35" 36 - 45 = "36 -45" 46 - high = "46, +"; goptions reset=all; proc gplot data=a; plot sf_Vt*time=id / haxis = 0 to 40 by 5 vaxis = 0 to 70 by 10 nolegend; plot 2 sf_vt*time=age / haxis = 0 to 40 by 5 vaxis = 0 to 70 by 10; symbol 1 v=none repeat=60 i=join color=red; symbol 2 v=none i=sm 50 s color=green width=3 line=1; symbol 3 v=none i=sm 50 s color=blue width=3 line=2; symbol 4 v=none i=sm 50 s color=magenta width=3 line=3; format agegrp. ; label time= "Time since baseline"; title "Individual Profiles and agegrp"; 46 run; quit;

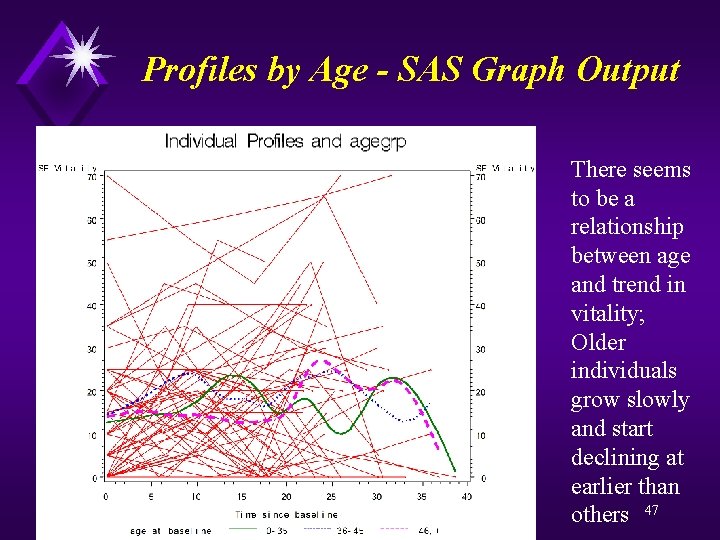
Profiles by Age - SAS Graph Output There seems to be a relationship between age and trend in vitality; Older individuals grow slowly and start declining at earlier than others 47

Profiles by Time Varying Covariates Baseline relationships- SAS Code Proc sort; by id flup; data baseline ; set a(rename=(sf_vt=base_sf_vtbdi_deprn=base_bdi_deprn)); by id; if (first. id) then do; keep id base_sf_vt base_bdi_deprn; output; end; goptions reset=all; proc gplot data=baseline; plot base_sf_vt*base_bdi_deprn / vaxis = 0 to 70 by 10 haxis = 0 to 40 by 5; plot 2 base_sf_vt*base_bdi_deprn / vaxis = 0 to 70 by 10 haxis = 0 to 40 by 5; symbol 1 v=circle color=red; symbol 2 v=none i=sm 50 s color=green width=5; label base_sf_vt = 'Baseline Vitality' base_bdi_deprn = 'Baseline BDI depression'; title 'Baseline Vitality and Baseline Depression'; run; quit; 48

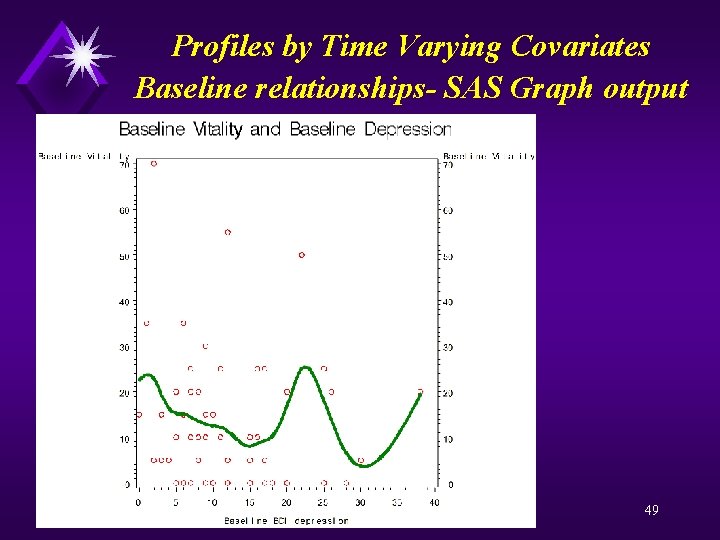
Profiles by Time Varying Covariates Baseline relationships- SAS Graph output 49

Profiles by Time Varying Covariates Longitudinal relationships - SAS Code proc sort; by id flup; data changes ; set a; by id; if (first. id) then do; base_sf_vt = sf_vt; base_bdi_deprn = bdi_deprn; end; retain base_bdi_deprn base_sf_vt; if ~(first. id) then do; keep id chg_sf_vt chg_bdi_deprn; chg_sf_vt = sf_vt-base_sf_vt; chg_bdi_deprn = bdi_deprn-base_bdi_deprn; output changes; end; goptions reset=all; proc gplot data=changes; plot chg_sf_vt*chg_bdi_deprn / vref = 0 vaxis = -40 to 50 by 10 haxis = -30 to 20 by 5; plot 2 chg_sf_vt*chg_bdi_deprn / vref = 0 vaxis = -40 to 50 by 10 haxis = -30 to 20 by 5; symbol 1 v=circle color=red; symbol 2 v=none i=sm 50 s color=green width=5; label chg_sf_vt = 'chg in Vitality' chg_bdi_deprn = 'change BDI depression'; title 'Change in Vitality and change in Depression'; run; quit; 50

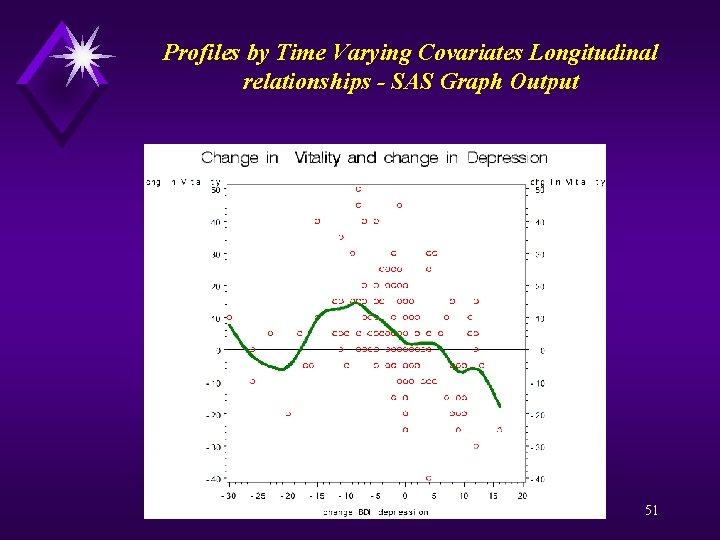
Profiles by Time Varying Covariates Longitudinal relationships - SAS Graph Output 51

Simple correlations- SAS Output proc corr data=a nosimple; var sf_vt time fm age bdi_deprn; title "Correlations - All observations"; proc corr data=changes nosimple; var chg_sf_vt chg_bdi_deprn; title "Correlation of change scores -time varying covariates"; proc corr data=baseline nosimple; var base_sf_vt base_bdi_deprn; title "Correlation baseline vitality baseline depression"; run; quit; 52

Simple correlations- SAS Output Pearson Correlation Coefficients, N = 239 Prob > |r| under H 0: Rho=0 sf_vt time fm age bdi_deprn sf_vt 1. 00000 0. 09511 -0. 17586 0. 04314 -0. 26315 SF-Vitality 0. 1426 0. 0064 0. 5069 <. 0001 time 0. 09511 1. 00000 0. 00911 -0. 00846 0. 11135 0. 1426 0. 8886 0. 8965 0. 0859 fm -0. 17586 0. 00911 1. 00000 -0. 16463 0. 20196 FM 0. 0064 0. 8886 0. 0108 0. 0017 age 0. 04314 -0. 00846 -0. 16463 1. 00000 0. 00935 age at baseline 0. 5069 0. 8965 0. 0108 0. 8857 bdi_deprn -0. 26315 0. 11135 0. 20196 0. 00935 1. 00000 Becker Depression inventory <. 0001 0. 0859 0. 0017 0. 8857 53

Simple correlations- SAS Output Pearson Correlation Coefficients, N = 179 Prob > |r| under H 0: Rho=0 chg_ bdi_ chg_ sf_vt deprn chg_sf_vt 1. 00000 -0. 25419 0. 0006 chg_bdi_deprn -0. 25419 1. 00000 0. 0006 2 Variables: base_ sf_vt base_bdi_deprn Pearson Correlation Coefficients, N = 60 Prob > |r| under H 0: Rho=0 base_ bdi_ sf _vt deprn base_sf_vt 1. 00000 -0. 11854 SF-Vitality 0. 3670 base_bdi_deprn -0. 11854 1. 00000 Becker Depression inventory 0. 3670 54

Summary of Exploratory Analysis u There may be a quadratic relationship between time and vitality u Although baseline scores are somewhat similar between those with FM and not with FM, VT scores of those with FM start to decline at an earlier time point u Older individuals seem to have a slower rate of increase in vitality and faster decline in vitality u A negative relationship exists between changes in depression and changes in vitality scores 55

About PROC MIXED u Can model random and mixed effect data, repeated measures, spatial data, data with heterogeneous variances and autocorrelated observations u 3 methods of estimation – u ML (Maximum Likelihood) u REML (Restricted or Residual maximum likelihood, which is the default method) and u MIVQUE 0 (Minimum Variance Quadratic Unbiased Estimation) 56

Covariance Pattern – SAS Code data a; set examples. mixed; if (int(age) < 35) then agegrp = 1; else if (35= < int(age) < 45) then agegrp = 2; else if (int(age) >= 45) then agegrp = 3; proc format; value agegrp 1 = "Lt 35" 2 = "35 -45" 3 = ">45"; proc mixed data=a; class id fm agegrp; model sf_vt = time*time fm agegrp bdi_deprn/ s ddfm=kr; format agegrp. ; repeated /sub=id type=cs r rcorr; title 'Longitudinal Model with Compound Symmetry Covariance Structure' run; quit; 57

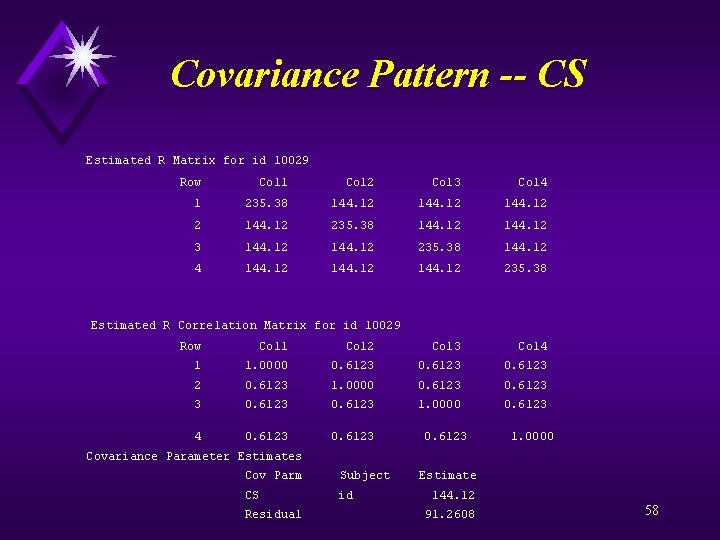
Covariance Pattern -- CS Estimated R Matrix for id 10029 Row Col 1 Col 2 Col 3 Col 4 1 235. 38 144. 12 2 144. 12 235. 38 144. 12 3 144. 12 235. 38 144. 12 4 144. 12 235. 38 Estimated R Correlation Matrix for id 10029 Row Col 1 Col 2 Col 3 Col 4 1 1. 0000 0. 6123 2 0. 6123 1. 0000 0. 6123 3 0. 6123 1. 0000 0. 6123 4 0. 6123 1. 0000 Covariance Parameter Estimates Cov Parm Subject Estimate CS id 144. 12 Residual 91. 2608 58

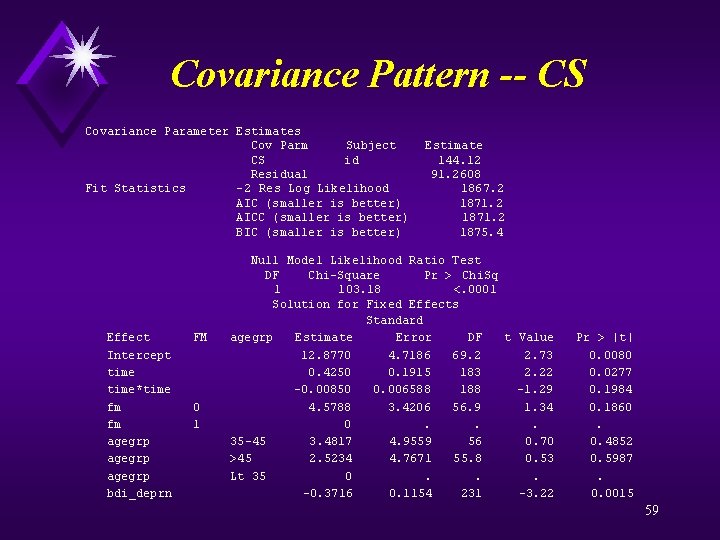
Covariance Pattern -- CS Covariance Parameter Estimates Cov Parm Subject Estimate CS id 144. 12 Residual 91. 2608 Fit Statistics -2 Res Log Likelihood 1867. 2 AIC (smaller is better) 1871. 2 AICC (smaller is better) 1871. 2 BIC (smaller is better) 1875. 4 Null Model Likelihood Ratio Test DF Chi-Square Pr > Chi. Sq 1 103. 18 <. 0001 Solution for Fixed Effects Standard Effect FM agegrp Estimate Error DF t Value Pr > |t| Intercept 12. 8770 4. 7186 69. 2 2. 73 0. 0080 time 0. 4250 0. 1915 183 2. 22 0. 0277 time*time -0. 00850 0. 006588 188 -1. 29 0. 1984 fm 0 4. 5788 3. 4206 56. 9 1. 34 0. 1860 fm 1 0 . . agegrp 35 -45 3. 4817 4. 9559 56 0. 70 0. 4852 agegrp >45 2. 5234 4. 7671 55. 8 0. 53 0. 5987 agegrp Lt 35 0 . . bdi_deprn -0. 3716 0. 1154 231 -3. 22 0. 0015 59

Random Intercept, Slope Model (SAS Code) proc mixed covtest method=reml noclprint; class id; model sf_vt = time / s; random intercept time /sub=id type=un gcorr; run; quit; 60

GL Mixed Model Building proc mixed covtest method=reml noclprint; class id; model sf_vt = time*time / s; random intercept /sub=id type=un gcorr; proc mixed covtest method=reml noclprint; class id fm; model sf_vt = time*time fm/ s; random intercept /sub=id type=un gcorr; proc mixed covtest method=reml noclprint; class id fm agegrp; model sf_vt = time*time fm agegrp/ s; format agegrp. ; random intercept /sub=id type=un gcorr; proc mixed covtest method=reml noclprint; class id fm agegrp; model sf_vt = time*time fm agegrp bdi_deprn/ s; format agegrp. ; random intercept /sub=id type=un gcorr; run; quit; 61

Model Summary 62

Interpreting Random Intercept, Slope models of the total variability in vitality over time and across people is due to between person differences or individual differences u The remainder 39% is how much people vary from themselves over time. u The variance of the intercept was the estimated variance of the individual deviations from the overall intercept and was significantly different from zero, reflecting significant individual differences in vitality u The variance estimate for the slope was not significantly different from zero, indicating that 63 u 61%

Summary of Findings u The model with random intercepts, and time as fixed effects with a quadratic term seems to best describe the differences in vitality scores and changes in vitality over time u No relationship between Age and vitality u No relationship exits between FM and vitality u Depression was negatively associated with vitality 64

What if we had done OLS ? Dependent Variable: sf_vt SF-Vitality Analysis of Variance Sum of Mean Source DF Squares Square F Value Pr > F Model 6 6446. 48084 1074. 41347 4. 69 0. 0002 Error 232 53106 228. 90620 Corrected Total 238 59553 Root MSE 15. 12965 R-Square 0. 1082 Dependent Mean 16. 88285 Adj R-Sq 0. 0852 Coeff Var 89. 61550 Parameter Estimates Parameter Standard Variable Label DF Estimate Error t Value Intercept 1 18. 20446 3. 16026 5. 76 time 1 0. 36910 0. 28883 1. 28 timesq 1 -0. 00615 0. 00959 -0. 64 fm* FM 1 -4. 23316 2. 03175 -2. 08 agegrp 2 1 3. 73914 2. 91263 1. 28 agegrp 3 1 2. 61273 2. 79285 0. 94 bdi_deprn** Becker Depression inventory 1 -0. 46112 0. 11980 -3. 85 <. 0001 0. 2026 0. 5217 0. 0383 0. 2005 0. 3505 0. 0002 65

References Charlie Hallahan, Sigstat HLM workshop – Rodenbush Book on HLM – Byrk and Rodenbush Proc Mixed – SAS Manual J Singer – Growth Models SUGI 66

moonbodly1985.blogspot.com

Source: https://slidetodoc.com/analysis-of-longitudinal-data-continuous-response-part-1/